mel语初解之二-多边型建模(3)
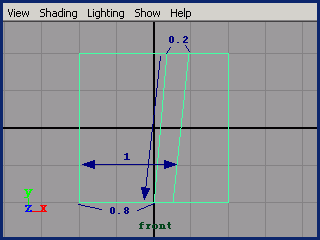
我们可以先把切割的百分比设置一个固定的数值,设为0.2(20%)。我们可以通过edge2Vertex()来得到要切割的一条边
的起点和终点,如果起点恰好是当初选择的那条边线的一个端点(两条边的公共点),那么这条线的构造顺序是正的,可以直接
使用20%;但如果构造顺序是反的,那就要使用1-20%=80%了。
这个函数应该这么写:proc splitByPercent(string $edge1, string $edge2, string $inputEdge)[注] 使用evalEcho执行命令可以把命令字符串在mel历史窗中显示出来。
{
// 预设值,百分比为0.2
float $percent = 0.2;
float $percent1 = $percent; // 0.2
float $percent2 = $percent; // 0.2
// 分别获得三条边所包含的顶点
string $verts1[], $verts2[], $vInput[];
$vInput = edge2Vertex($inputEdge);
$verts1 = edge2Vertex($edge1);
$verts2 = edge2Vertex($edge2);
// 求$edge1与$inputEdge的公共点
string $startVert[] = intersectStringArray($verts1, $vInput);
// 如果公共点不是$edge1的起点
if ($startVert[0] != $verts1[0])
// 百分比变为80%,即1-0.2
$percent1 = 1 - $percent;
// 求$edge2与$inputEdge的公共点
string $startVert[] = intersectStringArray($verts2, $vInput);
if ($startVert[0] != $verts2[0])
$percent2 = 1 - $percent;
// 获得两条边的索引号
string $index1 = getIndex($edge1);
string $index2 = getIndex($edge2);
// 准备命令字符串
string $cmd = "polySplit -ch on -s 1 ";
$cmd += "-ep " + $index1 + " " + $percent1 + " ";
$cmd += "-ep " + $index2 + " " + $percent2 + " ";
$cmd += ";";
// 选择整个多边形物体
string $polyName = getBaseName($edge1);
select -r $polyName;
// 执行命令
evalEcho($cmd);
}
第四步,切割边线两边的面。
有了前面的准备工作,最后一步就显得比较容易了。
global proc myEdgeChamfer()
{
// 获取选择的一条边
string $edges[] = getSelEdges();
string $inputEdge = $edges[0];
// 获取选择的边相邻的两个面
string $faces[] = getFaces();
// 等比切割第1个面
string $splitEdges[];
$splitEdges = adjacentEdgesInFace($faces[0], $inputEdge);
splitByPercent($splitEdges[0], $splitEdges[1], $inputEdge);
// 等比切割第2个面
$splitEdges = adjacentEdgesInFace($faces[1], $inputEdge);
splitByPercent($splitEdges[0], $splitEdges[1], $inputEdge);
}
附全部源代码。///////////////////////////////////////////////////////////
// myEdgeChamfer.mel
// myEdgeChamfer v1
// 获取选择的多边形顶点
proc string[] getSelVerts()
{
return `filterExpand -ex true -sm 31`;
}
// 获取选择的多边形边
proc string[] getSelEdges()
{
return `filterExpand -ex true -sm 32`;
}
// 获取选择的多边形面
proc string[] getSelFaces()
{
return `filterExpand -ex true -sm 34`;
}
// 根据点、边、面、UV点的名称得出多边形的名称
// 例如多边形一条边的名称为"pSphere1.e[637]",则这个多边形的
// 名称为"pSphere1"
proc string getBaseName(string $item)
{
string $buffer[];
if ($item != "")
{
tokenize($item, ".", $buffer);
}
return $buffer[0];
}
// 根据点、边、面、UV点的名称得出它们的索引号
// 例如多边形一条边的名称为"pSphere1.e[637]",则这个多边形的
// 索引号为637
proc int getIndex(string $indexString)
{
string $buffer[];
tokenize($indexString, "[]", $buffer);
int $index = (int)$buffer[1];
return $index;
}
// 获得两个数组的共同部分
proc string[] intersectStringArray(string $array1[], string $array2[])
{
global string $m_arrayIntersector;
if ($m_arrayIntersector == "")
$m_arrayIntersector = `stringArrayIntersector`;
stringArrayIntersector -edit -intersect $array1 $m_arrayIntersector;
stringArrayIntersector -edit -intersect $array2 $m_arrayIntersector;
string $result[] = `stringArrayIntersector -query $m_arrayIntersector`;
stringArrayIntersector -edit -reset $m_arrayIntersector;
return $result;
}
///////////////////////////////////////////////////////////
// 第一步,根据一条边,得到这条边的按构造顺序排列的两个端点。
proc string[] edge2Vertex(string $edge)
{
string $verts[], $buffer[];
string $edgeInfo[] = `polyInfo -ev $edge`;
int $nbVertex = tokenize($edgeInfo[0], $buffer);
string $polyName = getBaseName($edge);
$verts[0] = $polyName + ".vtx[" + $buffer[2] + "]";
$verts[1] = $polyName + ".vtx[" + $buffer[3] + "]";
return $verts;
}
// 已知一个面,这个面的一条边,求与(这个面的)这条边相邻的两条边
proc string[] adjacentEdgesInFace(string $face, string $edge)
{
// 获取所有相邻的边线
select -r $edge;
ConvertSelectionToVertices();
ConvertSelectionToEdges();
select -d $edge;
string $edges_vert[] = getSelEdges();
// 获取已知面的所有边线
select -r $face;
string $edges_face[] = getEdges();
// 求两个数组的共同部分
string $edges[] = intersectStringArray($edges_vert, $edges_face);
return $edges;
}
// 第三步,等比切割一个面
proc splitByPercent(string $edge1, string $edge2, string $inputEdge)
{
// 预设值,百分比为0.2
float $percent = 0.2;
float $percent1 = $percent; // 0.2
float $percent2 = $percent; // 0.2
// 分别获得三条边所包含的顶点
string $verts1[], $verts2[], $vInput[];
$vInput = edge2Vertex($inputEdge);
$verts1 = edge2Vertex($edge1);
$verts2 = edge2Vertex($edge2);
// 求$edge1与$inputEdge的公共点
string $startVert[] = intersectStringArray($verts1, $vInput);
// 如果公共点不是$edge1的起点
if ($startVert[0] != $verts1[0])
// 百分比变为80%,即1-0.2
$percent1 = 1 - $percent;
// 求$edge2与$inputEdge的公共点
string $startVert[] = intersectStringArray($verts2, $vInput);
if ($startVert[0] != $verts2[0])
$percent2 = 1 - $percent;
// 获得两条边的索引号
string $index1 = getIndex($edge1);
string $index2 = getIndex($edge2);
// 准备命令字符串
string $cmd = "polySplit -ch on -s 1 ";
$cmd += "-ep " + $index1 + " " + $percent1 + " ";
$cmd += "-ep " + $index2 + " " + $percent2 + " ";
$cmd += ";";
// 选择整个多边形物体
string $polyName = getBaseName($edge1);
select -r $polyName;
// 执行命令
evalEcho($cmd);
}
// 第四步,切割选择的一条边线两边的面。
global proc myEdgeChamfer()
{
// 获取选择的一条边
string $edges[] = getSelEdges();
string $inputEdge = $edges[0];
// 获取选择的边相邻的两个面
string $faces[] = getFaces();
// 等比切割第1个面
string $splitEdges[];
$splitEdges = adjacentEdgesInFace($faces[0], $inputEdge);
splitByPercent($splitEdges[0], $splitEdges[1], $inputEdge);
// 等比切割第2个面
$splitEdges = adjacentEdgesInFace($faces[1], $inputEdge);
splitByPercent($splitEdges[0], $splitEdges[1], $inputEdge);
}
 myEdgeChamfer_v1.rar (1.46k)
myEdgeChamfer_v1.rar (1.46k)
等距切割

要想知道一条边的长度,如果是Maya5.0或更低版本,可以使用arclen命令,但是到了Maya6.0,arclen命令只支持Nurbs,退化了?
这样我们不得不用到获得两点之间的距离的功能来计算边的长度。现在要提到一点图形学知识,当然是最最基础的,就是"勾股定理"。相信大家都能记得一点"勾股定理"的内容,我就不详细讲了。如果需要详细讲的话,可以提出来,我可以在后面补充。
"勾股定理"的公式是: a2 + b2 = c2
根据这个公式推理出3D空间勾股定理公式:x2 + y2 + z2 = d2
如果求两点之间的距离,公式如图:dist为点P1(x1,y1,z1)和P2(x2,y2,z2)之间的距离

根据公式,我们来编一个工具函数求两点之间的距离。你也许会感到奇怪,这么常用的功能,Maya中为什么没有内置的命令呢?这一点我也感到奇怪,好在编写这样的功能非常简单。
// 计算两个顶点之间的距离
proc float distance2Verts(string $vert1, string $vert2)
{
// 获取两个顶点的坐标值
float $p1[] = `pointPosition $vert1`;
float $p2[] = `pointPosition $vert2`;
// 计算距离
float $distance;
float $v[3];
$v[0] = $p1[0] - $p2[0];
$v[1] = $p1[1] - $p2[1];
$v[2] = $p1[2] - $p2[2];
$distance = $v[0]*$v[0] + $v[1]*$v[1] + $v[2]*$v[2];
$distance = sqrt($distance);// 开方
return $distance;
}
[注] 获取点的坐标值还有一种方法是:
float $p1[] = `xform -q -ws -t $ver1`;
[注] 获取点的坐标值还有一种方法是:
float $p1[] = `xform -q -ws -t $ver1`;
现在只要把等比切割的函数改一改就差不多了,把splitByPercent()改为splitByDist()。我把没有改动的部分用灰绿色表示,重点看看改动的部分。
[注] dist为distance的缩写。
// 第三步,等距切割一个面
proc splitByDist(string $edge1, string $edge2, string $inputEdge)
{
// 预设值,距离为0.2个单元格
float $dist = 0.2;
float $percent1;
float $percent2;
// 分别获得三条边所包含的顶点
string $verts1[], $verts2[], $vInput[];
$vInput = edge2Vertex($inputEdge);
$verts1 = edge2Vertex($edge1);
$verts2 = edge2Vertex($edge2);
// 计算第一条边的切割处
float $edgeLength; // 求第一条边的长度
$edgeLength = distance2Verts($verts1[0], $verts1[1]);
if ($edgeLength < $dist) // 如果长度小于预设值0.2
$percent1 = 1; // 切割处在线的的末端
else
$percent1 = $dist / $edgeLength; // 计算出百分比
// 计算第二条边的切割处
$edgeLength = distance2Verts($verts2[0], $verts2[1]);
if ($edgeLength < $dist)
$percent2 = 1;
else
$percent2 = $dist / $edgeLength;
// 求$edge1与$inputEdge的公共点
string $startVert[] = intersectStringArray($verts1, $vInput);
// 如果公共点不是$edge1的起点
if ($startVert[0] != $verts1[0])
// 百分比变为1-$percent1
$percent1 = 1 - $percent1;
// 求$edge2与$inputEdge的公共点
string $startVert[] = intersectStringArray($verts2, $vInput);
if ($startVert[0] != $verts2[0])
$percent2 = 1 - $percent2;
// 获得两条边的索引号
string $index1 = getIndex($edge1);
string $index2 = getIndex($edge2);
// 准备命令字符串
string $cmd = "polySplit -ch on -s 1 ";
$cmd += "-ep " + $index1 + " " + $percent1 + " ";
$cmd += "-ep " + $index2 + " " + $percent2 + " ";
$cmd += ";";
// 选择整个多边形物体
string $polyName = getBaseName($edge1);
select -r $polyName;
// 执行命令
evalEcho($cmd);
}
把distance2Verts()函数的定义加进去,再把myEdgeChamfer()函数中的两处splitByPercent()改为splitByDist(),这个程序就完成了。
附全部源代码。
 myEdgeChamfer_v2.rar (1.74k)
myEdgeChamfer_v2.rar (1.74k)
学习 · 提示
相关教程